Centre of Mass, Linear Momentum, Collision
Flashcards for topic Centre of Mass, Linear Momentum, Collision
Preview Cards
Front
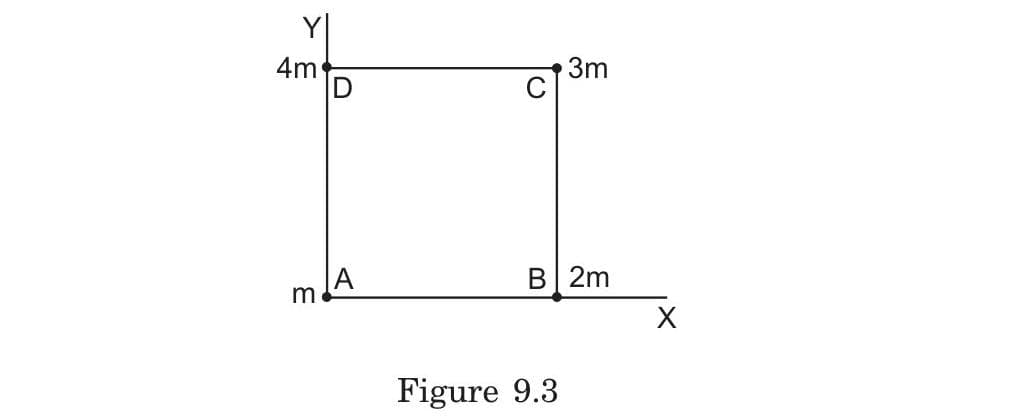
If the masses at the four corners of a square are in the ratio 1:2:3:4 (counterclockwise from bottom left), where precisely will the centre of mass be located relative to the square's dimensions?
Back
The centre of mass will be located at:
- Horizontally: exactly halfway across the square (at x = a/2, where a is the side length)
- Vertically: at 7/10 of the height (at y = 7a/10)
This position is biased toward the top-left corner where the 4m mass is located, and reflects how the centre of mass is weighted more heavily by larger masses.
Front
What happens to the velocities of two particles of different masses immediately after an inelastic collision, and how does this relate to the conservation principles?
Back
After a perfectly inelastic collision:
-
Both particles move with the same velocity V (they stick together)
-
This common velocity is determined from momentum conservation:
-
Kinetic energy is not conserved:
- Initial KE: ½m₁v₁² + ½m₂v₂²
- Final KE: ½(m₁+m₂)V² = ½(m₁+m₂)()²
- Final KE < Initial KE
-
The "lost" kinetic energy is converted to:
- Heat
- Sound
- Permanent deformation
- Internal energy of the combined system
Example: When a fast-moving clay ball hits a stationary clay ball, they stick together and move with reduced speed, with some kinetic energy converted to heat and deformation energy.
Front
What distinguishes the motion of a cricket ball's centre of mass from the motion of a point on its surface when the ball is spinning while in flight?
Back
- The centre of mass follows a simple, predictable path (parabolic trajectory under gravity), regardless of how the ball spins
- Points on the surface follow complex, non-planar paths resulting from the combination of:
- The overall translational motion of the ball
- The rotational motion around the centre of mass
- This distinction illustrates a fundamental principle: internal forces and motions (like spinning) cannot alter the path of the centre of mass, which responds only to external forces
- Example: A cricket ball thrown vertically upward while spinning will have its centre of mass move straight up and down, while a point on the surface traces a spiral path
Front
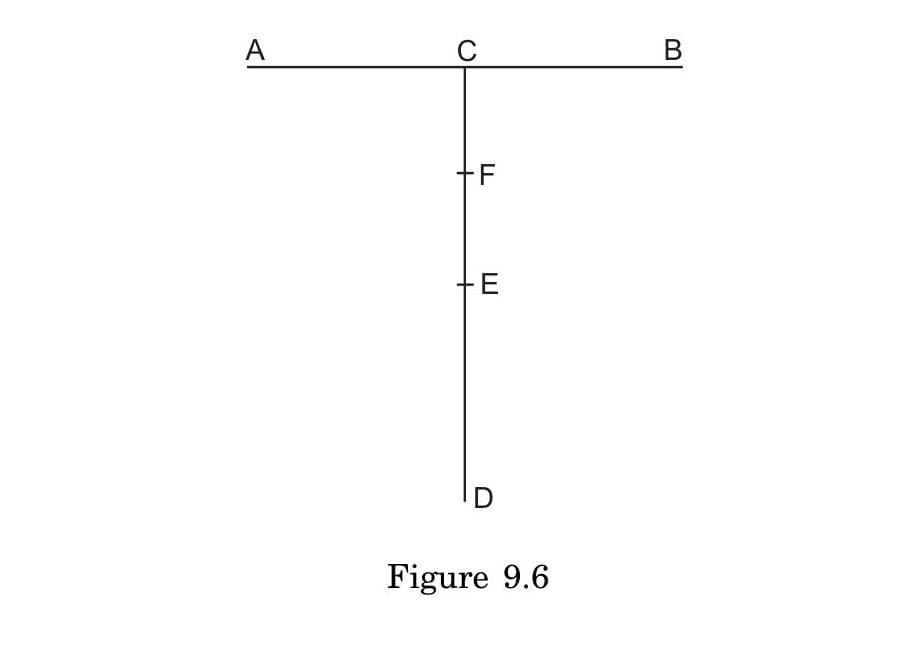
In a system composed of two uniform rods of equal mass arranged in a T-shape, what principle explains why the centre of mass is located on the vertical rod at a distance L/4 from the junction point?
Back
This location is explained by the principle of weighted position averaging:
-
For a system of multiple objects, the centre of mass divides the distance between individual centres of mass inversely proportional to their masses.
-
Mathematical explanation:
- Both rods have equal mass m
- Horizontal rod's centre of mass is at the junction point (0,0)
- Vertical rod's centre of mass is at distance L/2 from junction, along the vertical rod
- Combined CM position = (0 × m + 0 × m)/(m + m) for x-coordinate = 0
- Combined CM position = (0 × m + (L/2) × m)/(m + m) for y-coordinate = L/4
-
Alternatively: You can view this as replacing each rod with a point mass at its midpoint, then finding where these two point masses would balance.
The L/4 position reflects the equal "mass influence" of both rods while accounting for their geometric arrangement.
Front
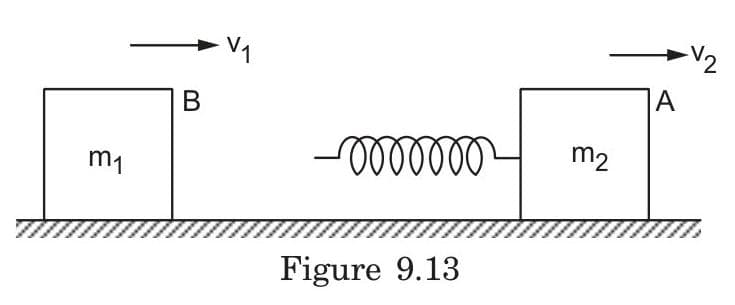
What is the key principle that determines when maximum spring compression occurs during a collision between two objects connected by a spring?
Back
- Maximum spring compression occurs precisely when both objects attain equal velocities
- This follows from conservation of momentum principles
- At this point:
- The relative velocity between objects becomes zero
- Both objects move with velocity V = (m₁v₁ + m₂v₂)/(m₁ + m₂)
- No further compression can occur since both ends of the spring move at identical speed
- The elastic potential energy stored in the spring equals the decrease in kinetic energy from the initial state
- Example: When a faster car (1000kg, 20m/s) rear-ends a slower car (800kg, 5m/s) with a bumper spring, maximum compression occurs when both move at 13.3m/s
Front
Compare and contrast what happens during a spring-mediated collision versus a direct collision between two objects, focusing on the momentum and energy principles.
Back
-
Common principles:
- Both collision types conserve total linear momentum
- Maximum deformation occurs when objects reach equal velocities
- The interaction force is internal to the system
-
Spring-mediated collision:
- Spring compression visibly shows energy storage
- Collision duration is extended and observable
- Force is proportional to displacement (F = kx)
- Final velocities: v'₁ = v₁-(2m₂(v₁-v₂))/(m₁+m₂), v'₂ = v₂+(2m₁(v₁-v₂))/(m₁+m₂)
-
Direct collision:
- Energy storage occurs through microscopic material deformation
- Perfectly elastic: Original shapes restore completely, initial KE = final KE
- Perfectly inelastic: Objects remain deformed, KE decreases, objects stick together
- Inelastic final velocity: v' = (m₁v₁+m₂v₂)/(m₁+m₂)
-
Example: Two billiard balls colliding directly demonstrate material deformation at microscopic levels, while two train cars with bumpers show a visible spring-mediated collision.

Front
What are the fundamental differences between elastic, partially elastic, and inelastic collisions in terms of energy and momentum conservation?
Back
| Collision Type | Momentum | Kinetic Energy | Mathematical Relationship | |---------------|----------|----------------|--------------------------| | Elastic | Conserved | Conserved | | | Partially Elastic | Conserved | Partially conserved | | | Perfectly Inelastic | Conserved | Maximum loss | Objects stick together: |
Key differences:
- Elastic: Objects separate after collision with no energy loss
- Partially Elastic: Objects separate with some energy converted to heat/sound
- Perfectly Inelastic: Objects stick together, maximum energy converted to other forms
For perfectly inelastic collisions, the common final velocity is:
Front
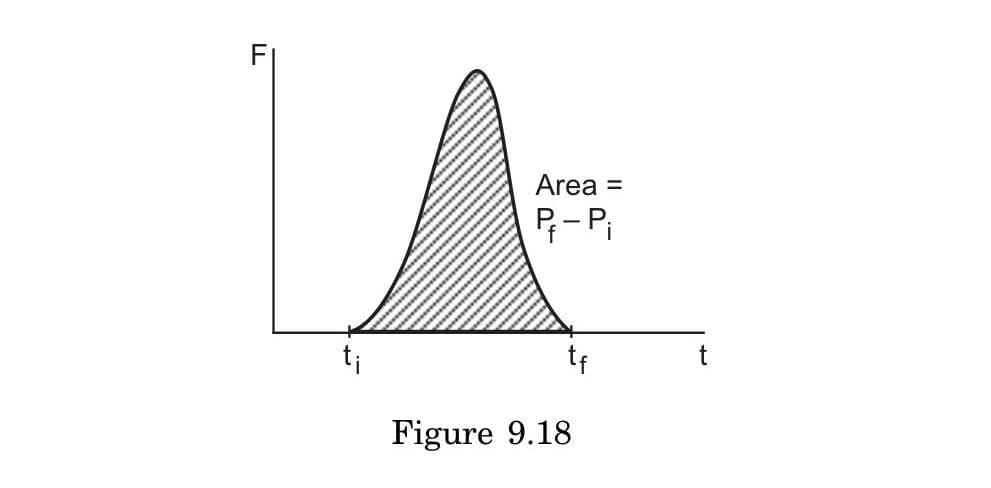
How does the area under a force-time curve relate to impulse and change in momentum?
Back
The area under a force-time curve represents impulse, which equals the change in momentum:
- Impulse =
- For constant force: Impulse =
- For variable force: Calculate the area under the F-t curve
- Units: N·s = kg·m/s
Example: In a car crash test, the force exerted on a crash test dummy varies with time. Engineers calculate the total impulse by finding the area under the F-t curve, which equals the change in the dummy's momentum during impact.
Note: The shape of the F-t curve matters - a longer duration with lower peak force can deliver the same impulse as a shorter duration with higher peak force, which is why airbags extend impact time to reduce peak forces.
Front
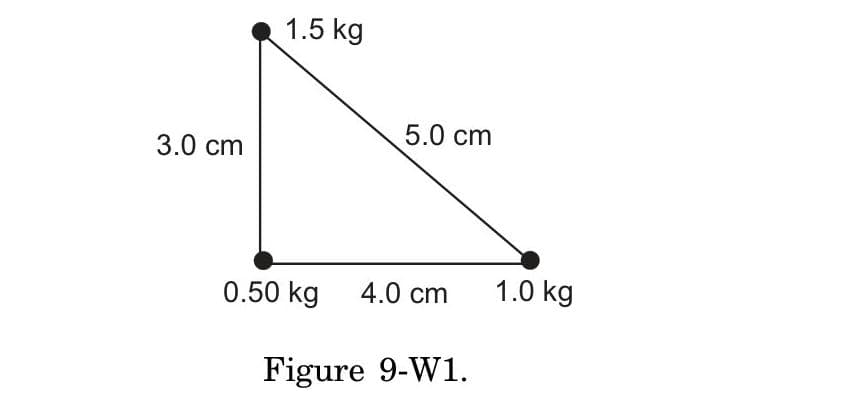
For a right-angled triangle with particles of different masses at each vertex, how does the position of the center of mass differ from the geometric center (centroid) of the triangle?
Back
The center of mass differs from the geometric center (centroid) in the following ways:
-
The geometric center (centroid) depends only on the triangle's shape and is located at the point where the medians intersect (⅓ of the way from each vertex to the midpoint of the opposite side)
-
The center of mass depends on both geometry AND mass distribution:
- It's pulled toward vertices with larger masses
- It can be located outside the triangle if mass distribution is heavily skewed
- It's calculated using weighted averages:
-
For uniform mass distribution (equal masses at each vertex), the center of mass coincides with the centroid
Note: The center of mass represents the unique point where the weighted relative position of the distributed mass sums to zero.
Front
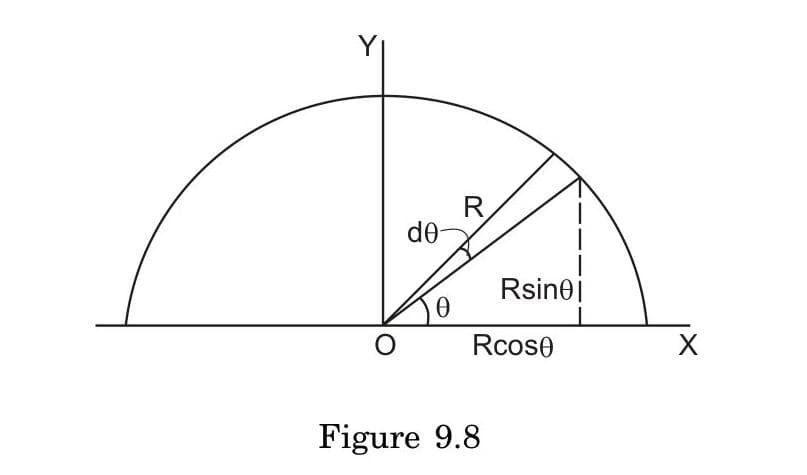
Compare and contrast the centres of mass for uniform semicircular objects: How and why do the positions differ for a semicircular wire versus a semicircular plate of radius R?
Back
Centre of Mass Positions
- Semicircular wire: (0, 2R/π) ≈ (0, 0.637R)
- Semicircular plate: (0, 4R/3π) ≈ (0, 0.424R)
- Geometric center of semicircle: (0, R/2) = (0, 0.5R)
Key Differences Explained
-
Dimensionality affects mass distribution:
- Wire: 1D object with mass distributed uniformly along arc length
- Plate: 2D object with mass proportional to area (more mass at larger radii)
-
Mathematical derivation:
- Wire: Y = ∫R·sinθ·(M/π)·dθ from θ=0 to π
- Plate: Y = ∫∫y·dm / M (with area element proportional to r·dr·dθ)
-
Physical interpretation:
- Wire's CM is higher (0.637R) because mass is concentrated along the curved path
- Plate's CM is lower (0.424R) because mass distribution extends throughout the area
- Both differ from the geometric center (0.5R) of the semicircle
-
Mass concentration visualization:
- Wire: Equal mass per unit arc length
- Plate: More mass at larger radii (area increases with distance from origin)
Note: These differences highlight how the dimensionality of an object fundamentally affects its mass distribution properties, even when the boundary shape is identical.
Showing 10 of 50 cards. Add this deck to your collection to see all cards.