Circular Motion
Flashcards for topic Circular Motion
Preview Cards
Front
Given a particle in non-uniform circular motion, derive the complete acceleration vector in terms of radial and tangential components.
Back
The complete acceleration vector has two perpendicular components:
-
Radial (centripetal) component: (directed toward center)
-
Tangential component: (tangent to circle)
Total acceleration magnitude:
Direction: Makes angle with radius where:
The radial component changes direction while tangential component changes speed.
Front
Distinguish between centripetal and centrifugal forces. When and why do we consider each one?
Back
• Centripetal force:
- Real force directed toward center of rotation
- Required for circular motion (provides necessary acceleration)
- Exists in inertial reference frames
- Examples: tension, friction, gravity, normal force
- Formula:
• Centrifugal force:
- Pseudo (fictitious) force appearing to act outward
- Only exists in rotating (non-inertial) reference frames
- Added to analysis to make Newton's laws applicable in rotating frames
- Formula: (outward direction)
- Not a "new" force, just a mathematical construct
Use centripetal force when analyzing from stationary/inertial frames, and include centrifugal force only when analyzing from the perspective of the rotating system.
Front
For a car traveling on a banked circular track, derive the relationship between the banking angle, speed, radius, and coefficient of friction for the maximum safe speed without skidding.
Back
For a car on a banked track with angle :
Without friction (ideal banking):
With friction (maximum safe speed):
Where:
- is speed
- is radius of turn
- is gravitational acceleration
- is banking angle
- is coefficient of static friction
Analysis:
- Normal force provides both vertical support and horizontal centripetal force
- Banking reduces or eliminates need for friction
- When speed exceeds ideal value, friction prevents outward skidding
- When speed is less than ideal, friction prevents inward skidding
- Maximum range of safe speeds:
Front
A conical pendulum makes a fixed angle with the vertical. Derive the relationship between the angle, length, angular speed, and period.
Back
For a conical pendulum (mass on string making angle with vertical while rotating):
Force analysis: • Tension: along string • Gravity: downward • Circular motion in horizontal plane of radius
Vertical equilibrium:
Horizontal (centripetal force):
From these:
Period:
Important relationships: • Larger angle → shorter period • Period depends on (similar to simple pendulum) • Horizontal circle radius: • Vertical height:
Front
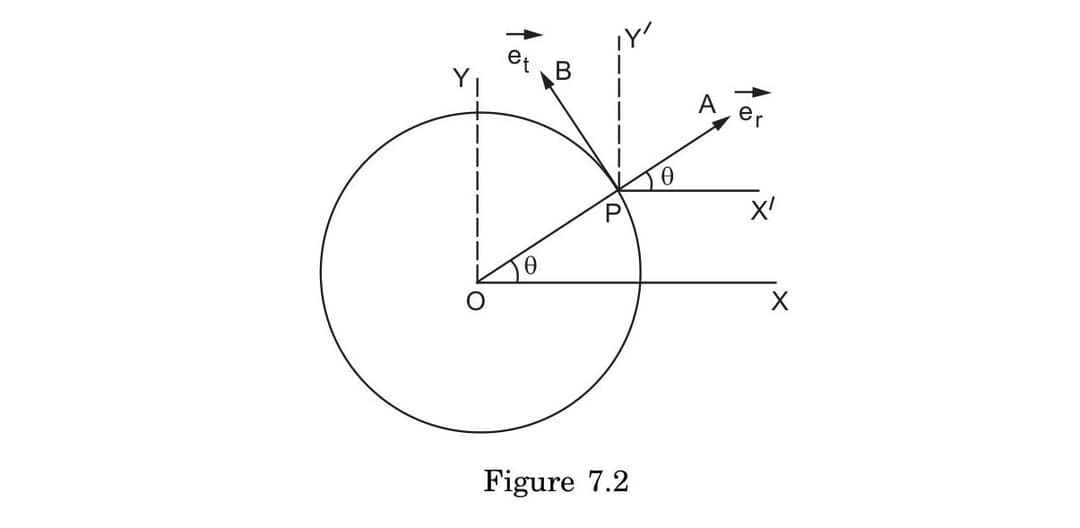
What are the unit vectors êr and êt in circular motion, and how are they defined in relation to a particle moving in a circle?
Back
- Radial unit vector (êr): Points outward along the radius from the center O to the particle P
- Tangential unit vector (êt): Points perpendicular to êr in the direction of increasing θ (tangent to the circle)
These unit vectors form a local coordinate system that moves with the particle, providing a natural basis for expressing forces and motion in circular paths.
Note: Unlike fixed Cartesian unit vectors (î, ĵ), these unit vectors continuously change direction as the particle moves around the circle.
Front
When analyzing acceleration in circular motion, how do the radial and tangential components relate to the unit vectors êr and êt, and what physical meaning does each component have?
Back
The acceleration in circular motion decomposes into:
-
Radial component: ar = -ω²r = -v²/r (points toward center, along -êr)
- Represents the centripetal acceleration
- Always present in circular motion, even at constant speed
- Changes the direction of velocity without changing its magnitude
-
Tangential component: at = dv/dt (points along êt)
- Represents change in speed of the particle
- Only present when speed is changing (non-uniform circular motion)
- Changes the magnitude of velocity without changing its direction
Example: A car rounding a curve while accelerating experiences both components: centripetal acceleration keeping it on the circular path and tangential acceleration increasing its speed.

Front
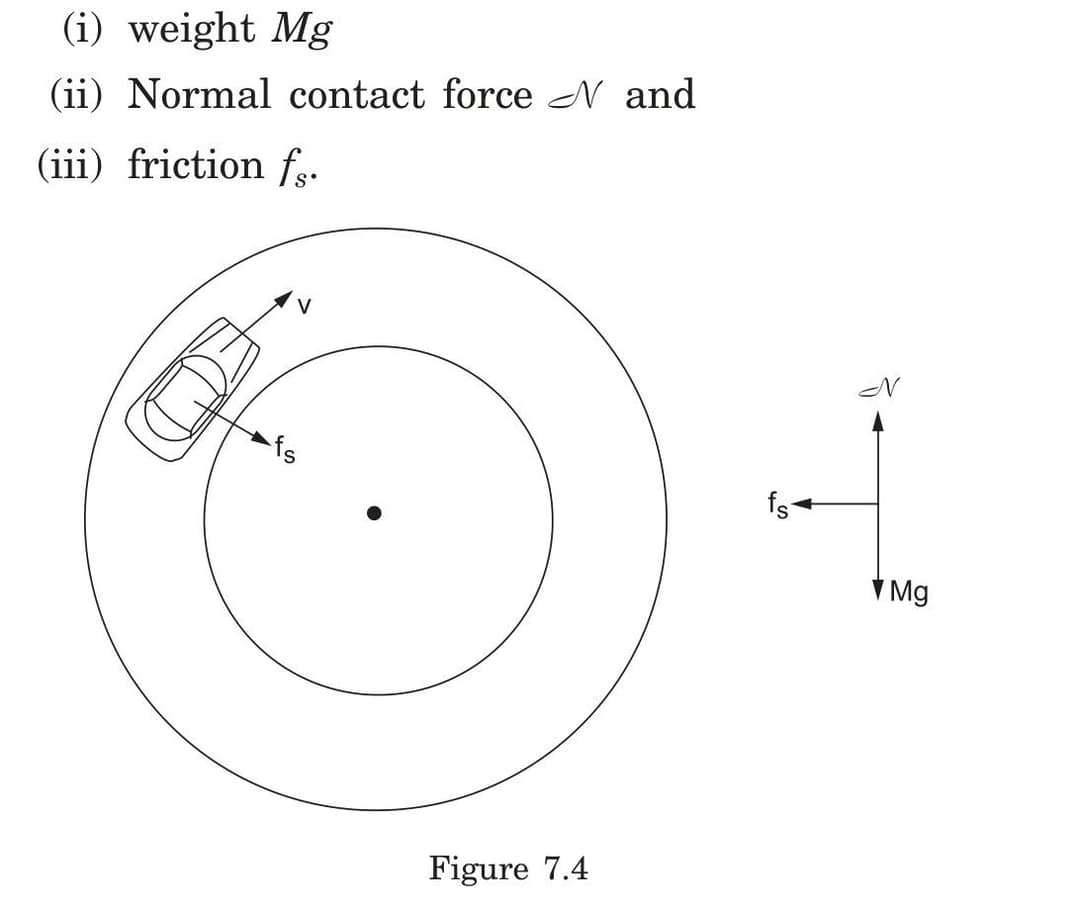
When a car travels around a horizontal circular turn, what specific condition must be met to prevent skidding, and how does this condition limit the maximum possible speed?
Back
To prevent skidding on a horizontal circular turn:
The static friction force must be sufficient to provide the required centripetal force:
- Required condition: fs ≥ mv²/r
- Maximum available friction: fs(max) = μs·N = μs·mg
When these are combined:
- μs·mg ≥ mv²/r
- v² ≤ μs·g·r
- vmax = √(μs·g·r)
This means:
- Maximum speed increases with larger turn radius (r)
- Maximum speed increases with higher friction coefficient (μs)
- Speed must be reduced on wet or icy roads (lower μs)
- Skidding occurs when the centripetal force requirement exceeds the maximum available friction
Real-world application: Highway design standards specify minimum turn radii based on expected speeds and typical friction coefficients.
Front
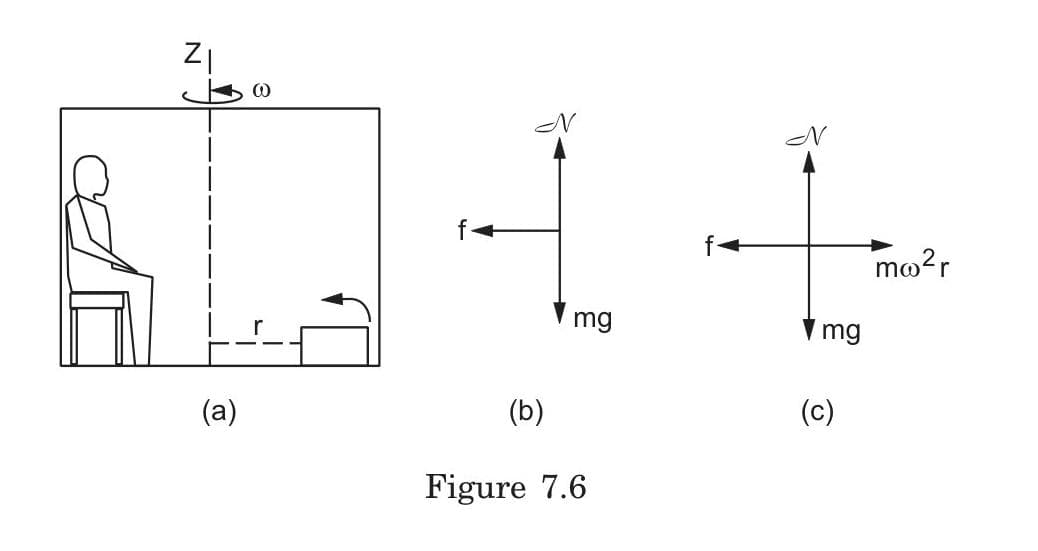
Compare and contrast how the same physical situation must be analyzed differently in (1) an inertial reference frame and (2) a rotating reference frame. Include the specific forces that must be considered in each case.
Back
Inertial Reference Frame Analysis:
- Only real forces are included (gravity, normal force, friction, etc.)
- For an object moving in a circle: Σ F = ma, where a = ω²r toward center
- Requires a real centripetal force to maintain circular motion
- The resultant force points toward the center of rotation
Rotating Reference Frame Analysis:
- Includes both real forces and pseudo forces
- For the same object: must add centrifugal force (mω²r outward)
- Allows application of Newton's laws within rotating frame
- For stationary objects in rotating frame: forces sum to zero
Example: For a box at rest on a rotating platform, from an inertial frame, friction provides the centripetal force keeping it moving in a circle. From the rotating frame, friction balances the centrifugal force, resulting in equilibrium.
Front
Calculate the magnitude of frictional force needed to keep a box of mass 2 kg from sliding in a rotating cabin with angular velocity 3 rad/s when the box is positioned 0.5 m from the rotation axis. Explain what this force physically represents in different reference frames.
Back
Calculation:
- Magnitude of required friction: f = mω²r
- f = (2 kg)(3 rad/s)²(0.5 m) = (2 kg)(9 rad²/s²)(0.5 m) = 9 N
Physical interpretation:
- In inertial frame: Friction provides the centripetal force (9 N inward) needed to keep the box moving in a circular path with proper acceleration
- In rotating frame: Friction (9 N inward) balances the centrifugal pseudo force (9 N outward), keeping the box stationary relative to the cabin
This demonstrates why a box appears stationary in a rotating reference frame despite actually undergoing circular motion - the frictional force provides exactly the acceleration needed to maintain circular motion when viewed from outside the rotating system.

Front
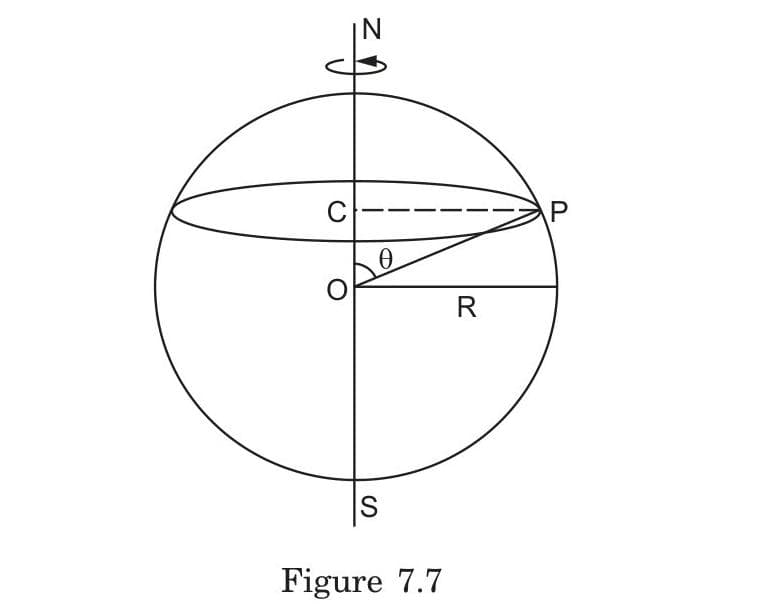
Calculate the ratio of centrifugal acceleration at a location with colatitude θ compared to the centrifugal acceleration at the equator.
Back
The ratio of centrifugal acceleration at colatitude θ to centrifugal acceleration at the equator is sin(θ).
Derivation:
- Centrifugal acceleration = ω²r
- At any location with colatitude θ: r = R·sin(θ)
- At the equator (θ = 90°): r = R
- Ratio = (ω²·R·sin(θ))/(ω²·R) = sin(θ)
For example:
- At 60° colatitude (30° latitude), the centrifugal acceleration is sin(60°) = 0.866 times that at the equator
- At 30° colatitude (60° latitude), the centrifugal acceleration is sin(30°) = 0.5 times that at the equator
This explains why apparent weight variation due to Earth's rotation changes with latitude.
Showing 10 of 33 cards. Add this deck to your collection to see all cards.